[Solution] Cross Swapping Codeforces Solution

E. Cross Swapping

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given a square matrix A$A$ of size n×n$n\times n$ whose elements are integers. We will denote the element on the intersection of the i$i$-th row and the j$j$-th column as Ai,j$A_{i,j}$.

You can perform operations on the matrix. In each operation, you can choose an integer k$k$, then for each index i$i$ (1≤i≤n$1\le i\le n$), swap Ai,k$A_{i,k}$ with Ak,i$A_{k,i}$. Note that cell Ak,k$A_{k,k}$ remains unchanged.

For example, for n=4$n=4$ and k=3$k=3$, this matrix will be transformed like this:

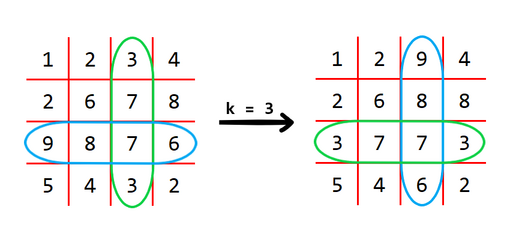The operation k=3$k=3$ swaps the blue row with the green column.

You can perform this operation any number of times. Find the lexicographically smallest matrix†${}^{†}$ you can obtain after performing arbitrary number of operations.

Solution Click Below:-  👉CLICK HERE👈

👇👇👇👇👇

 occupied

†${}^{†}$ For two matrices A$A$ and B$B$ of size n×n$n\times n$, let a(i−1)⋅n+j=Ai,j$a_{(i-1)\cdot n+j}=A_{i,j}$ and b(i−1)⋅n+j=Bi,j$b_{(i-1)\cdot n+j}=B_{i,j}$. Then, the matrix A$A$ is lexicographically smaller than the matrix B$B$ when there exists an index i$i$ (1≤i≤n2$1\le i\le n^2$) such that ai<bi$a_i<b_i$ and for all indices j$j$ such that 1≤j<i$1\le j<i$, aj=bj$a_j=b_j$.

Input

The first line contains a single integer t$t$ (1≤t≤105$1\le t\le {10}^5$) — the number of test cases.

The first line of each test case contains a single integer n$n$ (1≤n≤1000$1\le n\le 1000$) — the size of the matrix.

The i$i$-th line of the next n$n$ lines contains n$n$ integers Ai,1,Ai,2,…,Ai,n$A_{i,1},A_{i,2},\dots ,A_{i,n}$ (1≤Ai,j≤109$1\le A_{i,j}\le {10}^9$) — description of the matrix A$A$.

It is guaranteed that the sum of n2$n^2$ over all test cases does not exceed 106${10}^6$.

Output

For each test case, print n$n$ lines with n$n$ integers each — the lexicographically smallest matrix.