[Solution] Optimal Graph Partition for Fast Routing Codeforces Solution

GP1. Optimal Graph Partition for Fast Routing (GP1)

time limit per test

4 seconds

memory limit per test

512 megabytes

input

standard input

output

standard output

In computer networks, the Internet Protocol (IP) uses path routing. With path routing, the packet contains only the destination address; routers decide which "next hop" to forward each packet on to get it closer to its destination. Each router makes this decision locally, based only on the destination address and its local configuration. One way to store this configuration is to use routing tables, which means for each router, we store the "next hop" for every possible destination. However, as the scale of the network grows larger, the size of the router table grows as well. It is a big issue since routers only have limited computing resources. One way to address this issue is to divide the graph into several partitions.

For example, in the above figure, there are 12$12$ routers in the network. Each edge has a certain weight. Each router has to store 12$12$ table entries for all possible destinations in the network (including itself). We can merge four nodes in the graph into one large abstract node 𝑅2$R2$. When routers are merged, all existing edges connected to the elements of a large node are preserved. Then all routers outside 𝑅2$R2$ only need to store 9$9$ table entries. Therefore, in this case, we can assign the same "next hop" for all destination routers in 𝑅2$R2$. The intuition behind this is that router 𝑅1$R1$ does not need to care how to get 𝑅24$R24$ from 𝑅21$R21$ if 𝑅1$R1$ wants to send a packet to 𝑅24$R24$. 𝑅1$R1$ just needs to find a path to get its packet to an arbitrary router inside 𝑅2$R2$ and then let the routers inside 𝑅2$R2$ decide how to get 𝑅24$R24$. For routers inside 𝑅2$R2$, however, there are still 12$12$ table entries, because they need to know the routes to each other.

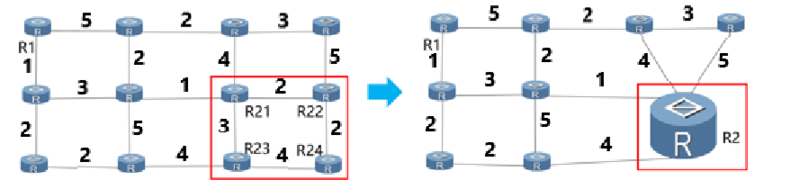
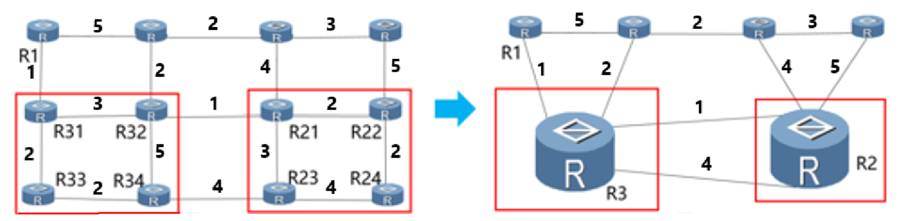
We can further merge 𝑅31,𝑅32,𝑅33,𝑅34$R31,R32,R33,R34$ into a single node 𝑅3$R3$. Then for 𝑅1$R1$, we need to store only 6$6$ entries in its routing table. For routers in 𝑅3$R3$ or 𝑅2$R2$, it only needs to store 9$9$ entries. Your task is to find an optimal partition of the initial graph to minimize the maximum size of the routing table for all routers in the network.

A computer network under consideration is an undirected connected graph 𝐺=(𝑉,𝐸)$G=(V,E)$, where |𝑉|=𝑁 (2≤𝑁≤105)$|V|=N(2\le N\le {10}^5)$, |𝐸|=𝑀 (1≤𝑀≤2×105)$|E|=M(1\le M\le 2\times {10}^5)$, 𝑉={0,1,…,𝑁−1}$V=\{0,1,\dots ,N-1\}$, 𝐸={𝑒=(𝑢,𝑣,𝑤)∣There is an edge between nodes 𝑢 and 𝑣 with weight 𝑤}.$E=\{e=(u,v,w)\mid$

$\text{There is an edge between nodes }u\text{ and }v\text{ with weight }w\}.$

A partition 𝑃$P$ of the network 𝐺$G$ is a set of non-empty subsets of 𝑉$V$ such that every node 𝑣∈𝑉$v\in V$ belongs to exactly one of these subsets, and the induced sub-graph for each subset in 𝑃$P$ is connected. Here, one subset corresponds to one abstract node mentioned above.

Formally, 𝑃$P$ is a valid partition if and only if 𝑃$P$ is a family of sets that satisfies:

• ∅∉𝑃$\mathrm{\varnothing }\notin P$
• ⋃𝐴∈𝑃𝐴=𝑉$\bigcup _{A\in P}A=V$
• ∀𝐴,𝐵∈𝑃:𝐴≠𝐵⟹𝐴∩𝐵=∅$\mathrm{\forall }A,B\in P:A\ne B⟹A\cap B=\mathrm{\varnothing }$
• ∀𝐴∈𝑃$\mathrm{\forall }A\in P$, the induced subgraph 𝐺[𝐴]$G[A]$ is connectedThe set 

𝐹𝐸(𝑃)$FE(P)$ of free edges of the partition 𝑃$P$ are those edges that are not part of the merged nodes, that is, those edges that connect the merged nodes. 𝑤(𝑒)$w(e)$ is the weight of the edge 𝑒$e$.

In this subtask, it is necessary to solve a narrowed bi-criteria optimization problem:The score for SubTask1 for the 

𝑖𝑡ℎ$i^{th}$ graph is calculated by the formula:

Input

The first line contains two integers 𝑁$N$ and 𝑀$M$ (2≤𝑁≤105;𝑁−1≤𝑀≤2×105)$(2\le N\le {10}^5;N-1\le M\le 2\times {10}^5)$ — the number of nodes and edges, respectively.

Each of the next 𝑀$M$ lines contains three integers 𝑢𝑖,𝑣𝑖$u_i,v_i$ and 𝑤𝑖$w_i$ (0≤𝑢𝑖, 𝑣𝑖≤𝑁−1, 𝑢𝑖≠𝑣𝑖, 1≤𝑤𝑖≤105$0\le u_i,v_i\le N-1,u_i\ne v_i,1\le w_i\le {10}^5$), denoting an edge between the node 𝑢𝑖$u_i$ and 𝑣𝑖$v_i$ with weight 𝑤𝑖$w_i$. 𝑒𝑖=(𝑢𝑖,𝑣𝑖,𝑤𝑖)$e_i=(u_i,v_i,w_i)$ is the edge with index 𝑖$i$ in the edge set 𝐸$E$. It is guaranteed that the input graph is connected and there are no multiple edges. That is, any pair (in any order) of nodes appear in this list no more than once.

Output

In the first line, output the number of subsets in your partition 𝑃$P$.

The (𝑖+1)$(i+1)$-th line should begin with a single number 𝑐𝑛𝑡𝑖$cn{t}_i$ — the size of the 𝑖$i$-th subset, followed by 𝑐𝑛𝑡𝑖$cn{t}_i$ numbers, denoting the node IDs in the 𝑖$i$-th subset.

Scoring

During the coding phase, your solutions are tested against pre-tests only. The first 5$5$ of them are open and available for download at the link problem-gp1-open-testset.zip in the "contest materials" section in a sidebar.

After the end of the coding phase, the last submission that scored a positive number of points on the pre-tests will be selected. It will be retested in the final tests. The rest of your submissions will be ignored. The final tests are secret and not available to the participants, they are mostly realistic. The result obtained on the final tests is your final official result for this problem.

1. According to the formula, the solution with a larger score wins.
2. If two solutions have the same score, the solution submitted first wins.